Uma imagem é uma representação visual de algum senário, de fato uma imagem pode conter informações muito valiosas, seja apenas para registrar um momento, uma comprovação de um fato ocorrido ou ate para automatizar uma tarefa.

Além de uma representação visual, é possível em condições específicas extrair informações de profundidade, isso é, a distância e cada pixel em relação à câmera. Mais como essa informação é obtida? Isso é que vamos ver nesse artigo.

Visualmente nós temos uma certa noção de profundidade, isso nós permitimo estimar a distância que estamos de um determinado objeto. Podemos fazer isso porque vemos o objeto de dois pontos de vista (olho direito e esquerdo). Então se colocar duas câmeras alinhadas podemos chegar nesse mesmo resultado.

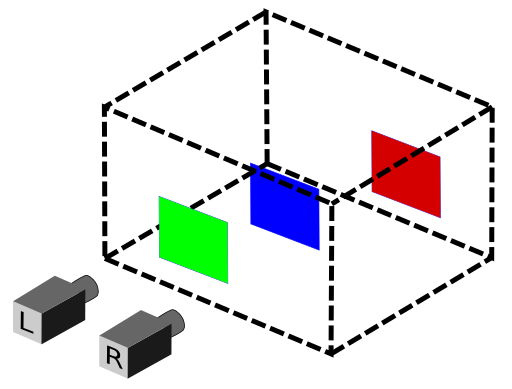
O sensor kinect do xbox e a série intelrealsense são câmeras de profundidade que explora justamente esse conceito.

Calculando profundidade.

Na prática, é impossível alinhar perfeitamente duas câmeras em uma mesma linha de base, mais podemos fazer isso via softwares, esse processo é conhecido com retificação de imagem, que nada mais é do que uma transformação de espaço. Às duas imagens são projetadas no mesmo espaço.

Devido o posicionamento das câmeras ocorre um pequeno desvio na posição em que cada pixel quando comparamos a imagem da esquerda com a direita, esse desvio é o que chamamos de disparidade.

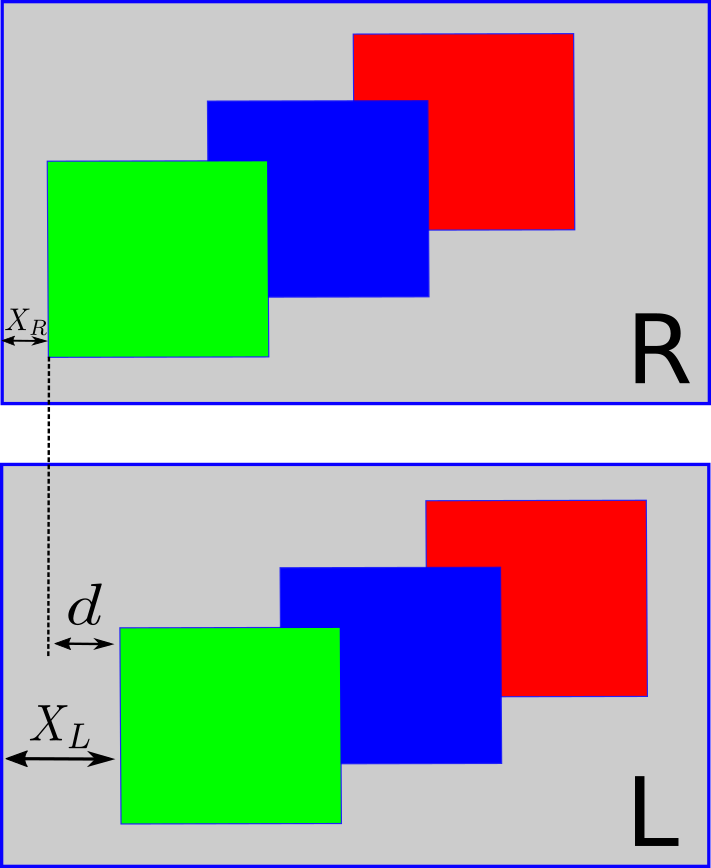
Então para calcular a disparidade, selecionamos na imagem da esquerda um pixel ou bloco de pixel e procuramos esse pixel na imagem da direita, O código a baixa faz isso para duas imagens, left e right (Fonte: https://github.com/IntelRealSense/librealsense/blob/master/doc/depth-from-stereo.md).

import cv2
import matplotlib.pyplot as plt
import numpy as np
img= cv2.imread("rectified.png")
left=img[:,:640,]
right=img[:,640:,]
fx = 942.8        # comprimento focal
baseline = 54.8   # distância mm entre as câmeras
disparities = 64  # limite máximo de disparidade 
block = 15        # Tamanho do bloco
units = 0.001     # fator para converter para metros
disparity=np.zeros(shape=left.shape[:2],dtype=np.uint8)
for i in range(block, left.shape[0] - block - 1):
    for j in range(block + disparities, left.shape[1] - block - 1):
        ssd = np.empty([disparities, 1])

        # calc SSD at all possible disparities
        l = left[(i - block):(i + block), (j - block):(j + block)]
        for d in range(0, disparities):
            r = right[(i - block):(i + block), (j - d - block):(j - d + block)]
            ssd[d] = np.sum((l[:,:]-r[:,:])**2)

        disparity[i, j] = np.argmin(ssd)

# Convert disparity to depth
depth = np.zeros(shape=left.shape).astype(float)
depth[disparity > 0] = (fx * baseline) / (units * disparity[disparity > 0])
plt.imshow(depth)
plt.show()

Se colocarmos um objeto muito próximo ao nariz, o que vemos com olho direito é um pouco diferente da visão do olho esquerdo, mais quando começamos a distanciar o objeto a tendência de que ambos os olhos tenham a mesma visão. 

Com um objeto próximo temos uma disparidade alta e com ele longe temos uma disparidade baixa. Ou seja, a disparidade é uma grandeza inversamente proporcional a distância, então se medirmos disparidade podemos calcular a distância.

Vamos pegar uma vista superior do nosso senário anterior

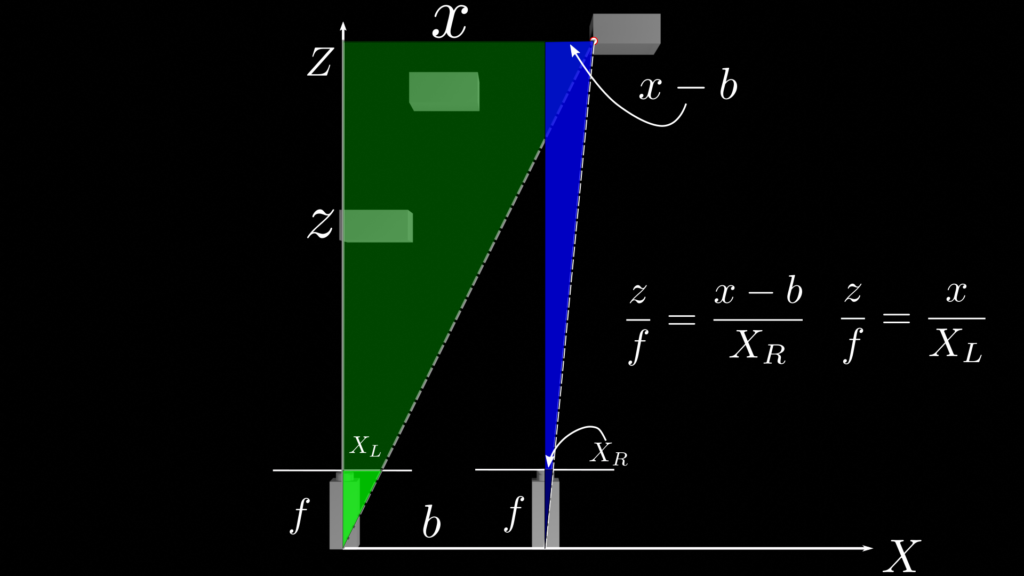
A distância entre o centro das câmeras é o que chamamos de base ($b$), também é a linha de referência em que as imagens devem ser retificadas.

Por semelhança de triângulos podemos dizer que $z$ esta para $f$ assim como $x$ esta para $X_L$.

\begin{equation}
\frac{z}{f}=\frac{x}{X_L}
\end{equation}

Para os triângulos azuis. $z$ esta para $f$ assim como $X-b$ está para $X_R$.

\begin{equation}
\frac{z}{f}=\frac{X-b}{X_R}
\end{equation}

Isolando $x$ da última equação, temos:

\begin{equation}
x=\frac{b*X_L}{X_L-X_R}
\end{equation}

Subistituindo $x$ na primeira equação, temos:

\begin{equation}
\frac{z}{f}=\frac{1}{X_L}\frac{b*X_L}{X_L-X_R}
\end{equation}

\begin{equation}
z=\frac{f*b}{X_L-X_R}
\end{equation}

A distância $z$ depende do comprimento focal $f$, da distância entre as câmeras e a disparidade entre as imagens.

Conclusão

Nesse post vimos como obtemos a profundidade de senário a partir de duas câmeras, é difícil dizer a aplicabilidade disso, já vemos em carro autônomos, drones, mais pode ser usado para medir comprimento e área de um objeto com isso ter uma compreensão muito mais completa de um senário.

Se você encontrou algum erro nesse post deixe nos comentários, também ficarei feliz em saber se esse post te ajudou.